Filtering Data in Syncs
Do take a look at Starting Syncs to get started with syncing data
If you want to filter the data that is being fetched in the syncs, you can use the Sync Filter APIs to provide relevant filters.
What is a Sync Filter?
A sync filter is essentially an expression tree that is evaluated for each record fetched from the source app.
For example, let's consider that we are syncing employee data and want to fetch the employees that belong to either the Technology or Marketing department.
Take a look at the event data example for
employeesync here
An expression tree for the above filter, keeping in mind the event data JSON, could look like this:
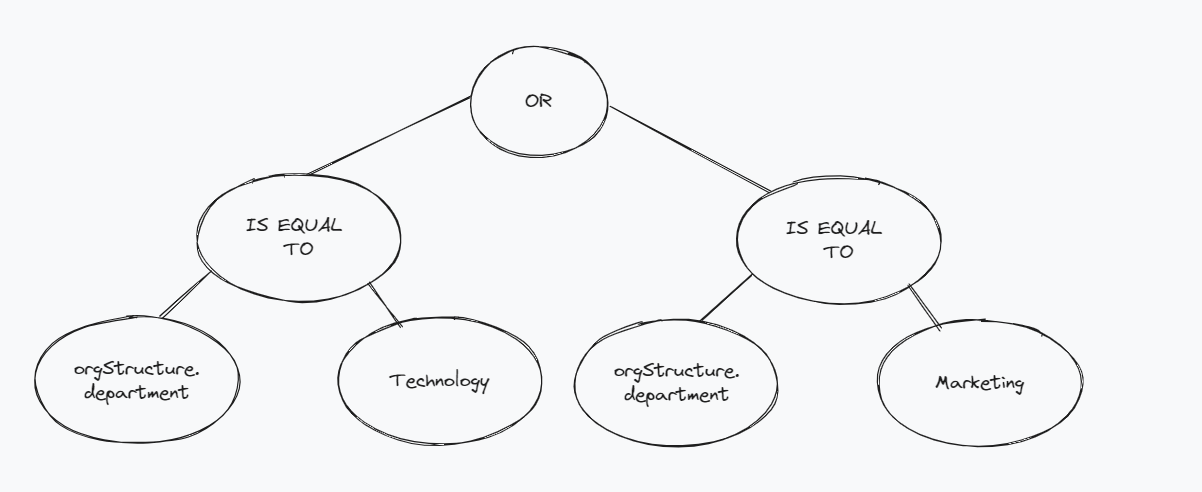
Since the department value is inside the orgStructure model, we represent nested values with dot (.) notation, and hence the key that we want to filter on becomes orgStructure.department
At the top, we have a logical operator or, and the left and right trees evaluate whether the department is equal to Technology or Marketing respectively. The above tree would evaluate to true if the employee's department is either Technology or Marketing, otherwise it would evaluate to false.
How to construct a Sync Filter?
A node in the JSON representation of the Sync Filter essentially has four parts:
| Key | Data Type |
|---|---|
data | String |
type | Enum |
left | Filter Node |
right | Filter Node |
Let's look at each one in detail.
data
The data key represents the operator/key/value that is being used while evaluating
type
The possible types are:
Type | Description | Possible Values |
|---|---|---|
| Logical Operators. Must have a left and right branch that is made up of other operators. |
|
| String Operators. Used to compare filter on keys that or type |
|
| Date operators are used to compare filter on keys that are of two types
|
|
| The node is a key | |
| The | |
| The |
Left And Right
Represent the left and right branches of the node. Can be null if the node is a leaf node.
Operators must have left and right branchesOperators like
logical_operator,date_operatorandstring_operatormust have both, a left branch and right branch to be properly evaluated
Let's construct the JSON representation of the following simple tree with just three nodes:
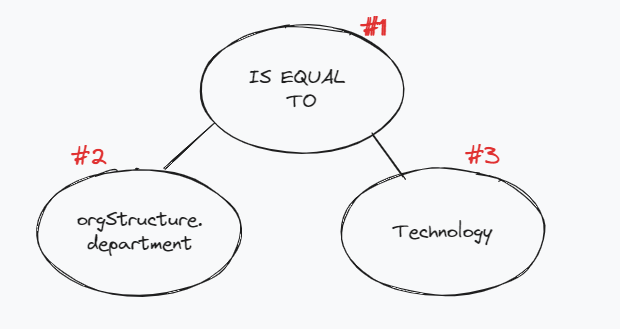
Starting from the bottom,
- Node #2 is the
keythat we want to compare against. Since the department value is inside theorgStructuremodel in the Employee Data Model, and we represent nested values withdot (.)notation, and hence the key that we want to filter on becomesorgStructure.department. From the model documentation, we also note that the data type of the key isString. The JSON representation of this node would look like this:-
{ "data": "orgStructure.department", "type": "key", "left": null, "right": null }
-
- Node #3 is the value that we want to be filtered. Previously, we noted the key
orgStructure.departmentis of typeString, hence we will specifyvalue_stringas the type here. The JSON representation of this node would look like this:-
{ "data": "Technology", "type": "value_string", "left": null, "right": null }
-
- To combine the two nodes we have created so for, we have an operator as the Node #1. Like the previous node, since we are doing
Stringcomparison, we specifystring_operatoras the type and in particular, since we want to compare the equality of the key - value, we will use theeqoperator.
Combining all the above nodes, a full JSON representation of the above tree would look like this:
{
"data": "eq",
"type": "string_operator",
"left": {
"data": "orgStructure.department",
"type": "key",
"left": null,
"right": null
},
"right": {
"data": "Technology",
"type": "value_string",
"left": null,
"right": null
}
}
Things to keep in mind while constructing a filter
- Nested keys are represented by dot(.) notation, eg,
orgStructure.department- Operators like
logical_operator,string_operatorand date_operator must have both, a left branch and right branch to be properly evaluated
logical_operatormust have a left and right branch that is made up of other operators.string_operatormust have a left and right branch, in which one is of typekeyand the other is of typevalue_stringdate_operatormust have left and right branch, in which one should be key and other will be one of among ,value_date(For Date type filter),value_string( For rolling time based filter).- Use the right operator type to make comparisons. For eg, If the key that you want to compare with is of type
String, then you must usestring_operatorwith it.
Now that we have our filter JSON ready, let's add it to the sync.
How to add filter to my integrations?
To add a filter to an integration, you can use the Update Sync Filter API to provide the filter JSON that we have just constructed.
Updating the filter triggers aninitial_syncWhen you update the filter using the above API, it would trigger an
initial_sync, so as to baseline the data with the new filter.You can use the
triggerSyncparameter to control this behavior.
That's it! You're all set with filtering data in syncs! Once you set a filter, all future delta_syncs for that integration will only track the data points that pass the filer, and thus you will be able to get targeted data from the syncs and keep better track of your data!
Updated 6 months ago